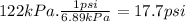Question

A closed tank is partially filled with seawater with density 1,030 kg/m3. If the pressure in the tank's airspace is 32 kPa and the depth of seawater is 9 m, what is the pressure at the bottom of the tank in Pa and psi (lb/in?)?

Answer 1

The pressure at the bottom is 122 kPa or 17.7 psi.

Step-by-step explanation:

The pressure at the bottom is equal to the pressure of the airspace plus the pressure of the seawater.

Pbottom = Pairspace + Pseawater [1]

The pressure caused by the column of seawater can be calculated using the expression:

Pseawater = ρ . g . h [2]

where,

ρ is the density of the seawater

g is the gravity (9.87 m/s²)

h is the depth of the seawater column

Solving [2]:

Pseawater = 1,030 kg/m³ x 9.87 m/s² x 9 m = 9 x 10⁴ kg/m.s² = 9 x 10⁴ Pa

`Pseawater=9* 10^(4) Pa.(1kPa)/(10^(3)Pa ) =90kPa`

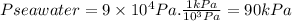
Then, we use this result in [1]:

Pbottom = Pairspace + Pseawater

Pbottom = 32 kPa + 90 kPa = 122 kPa

We can express this result in psi, knowing that 1 psi = 6.89 kPa.

`122kPa.(1psi)/(6.89kPa) =17.7psi`