Question

Using the Virial equations to second order, what is the molar volume Vm of Ar at 315.2 K when p = 53 atm? What is the compression factor, Z, under the same conditions?

Answer 1

Answer: The molar volume of the Argon is 0.321 L/mol and compression factor is 0.658

Step-by-step explanation:

To calculate the compression factor, we use the Virial equation to the second order, which is:

`Z=1+B'P+C'P^2`

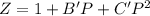
where,

Z = compression factor

B' = second virial constant =
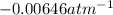`-0.00646atm^(-1)` (From standard values)

C' = third virial constant =
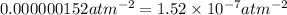`0.000000152atm^(-2)=1.52* 10^(-7)atm^(-2)` (From standard values)

P = pressure of the gas = 53 atm

Putting values in above equation, we get:

`Z=1+(-0.00616atm^(-1)* 53tm)+(1.52* 10^(-7)atm^(-2)* (53)^2)\\\\Z=0.658`

Now, calculating the molar volume, by using the equation of compression factor:

`Z=(PV_m)/(RT)`

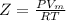
where,

Z = compression factor = 0.658

P = pressure of the gas = 53 atm

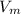`V_m` = molar volume of gas = ?

R = Gas constant =
`0.0821\text{ L atm }mol^(-1)K^(-1)`

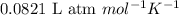
T = Temperature of the gas = 315.2 K

Putting values in above equation, we get:

`0.658=\frac{53atm* V_m}{0.0821\text{ L atm }mol^(-1)K^(-1)* 315.2K}\\\\V_m=\frac{0.658* 0.0821\text{ L atm }mol^(-1)K^(-1)* 315.2K}{53atm}=0.321L/mol`

Hence, the molar volume of the Argon is 0.321 L/mol and compression factor is 0.658