Answer:
Supplier B more likely supplied the defective materials.
Step-by-step explanation:
This exercise is solved in four steps:
1. Statistical events are defined:
A = (provider A)
B = (provider B)
D = defective materials
From the problem statement, 27% of the materials used by Company C are provided by supplier A. Therefore:
P (A) = 0.27.
The remaining 73% is provided by supplier B. Therefore:
P (B) = 0.73.
2. Conditional probabilities are established. In other words, what is the probability that the materials are defective? Remember that the "defect" is the condition that most interests the manager.
According to the example, 22% of materials from supplier A are defective. We can formalize this as follows:
P (D / A) = 0.22
On the other hand, 9% of supplier B materials are defective:
P (D / B) = 0.09
3. It will be determined what is the probability that each supplier has provided defective products by applying Bayes´ theorem.
3.1 The probability of this event will be found for supplier A:
The Bayes´ Theorem for this case is:
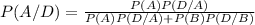
We replace with the data obtained in the previous points (1 and 2):
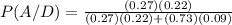


P (A / D) = 0.474
That means that approximately 47.4% of defective materials come from supplier A.
3.2 The probability of this event for provider B will be found.
The Bayes´ Theorem for this case is:
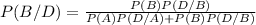
We replace with the data obtained in the previous points (1 and 2):
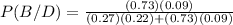

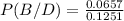
P (B / D) = 0.525
That means that approximately 52.5% of the defective materials come from supplier B.
4. Compare the conditional probabilities.
If we compare P (A / D) and P (B / D), we can see that the largest is P (B / D) (47.4 < 52.5). Therefore, supplier B is more likely to have supplied defective materials.