Question

Romi, a production manager, is trying to improve the efficiency of his assembly line. He knows that the machine is set up correctly only 60% of the time. He also knows that if the machine is set up correctly, it will produce good parts 80% of the time, but if set up incorrectly, it will produce good parts only 20% of the time. Romi starts the machine and produces one part before he begins the production run. He finds the first part to be good. What is the revised probability that the machine was set up correctly?

Answer 1

If the first part is good, there is a 85.71% probability that the machine was set up correctly.

Explanation:

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

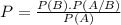
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

So, the question is:

What is the probability that the machine was set up corretcly, given that the first part is good?

P(B) is the probability that the machine was set up correctly. The problem states that the machine is set up correctly only 60% of the time. So P(B) = 0.6.

P(A/B) is the probability that the first part is good, given that the machine was set up correctly. The problem states that that if the machine is set up correctly, it will produce good parts 80% of the time, so P(A/B) = 0.8

P(A) is the probability that a good part is produced. The problem states that the machine is set up correctly only 60% of the time. He also knows that if the machine is set up correctly, it will produce good parts 80% of the time, but if set up incorrectly, it will produce good parts only 20% of the time. So:

P(A) = 0.6*0.8 + 0.4*0.2 = 0.56

Finally

`P = (P(B).P(A/B))/(P(A)) = (0.6*0.8)/(0.56) = 0.8571`

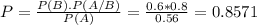
If the first part is good, there is a 85.71% probability that the machine was set up correctly.