Question

Consider the experiment, called the birthday problem , where our task is to determine the probability that in a group of people of a certain size there are at least two people who have the same birthday (the same month and day of month). Suppose there is a room with 9 people in it, find the probability that at least two people have the same birthday. Ignore leap years; assume each year has 365 days.

Answer 1

There is a 0.02% probability that at least two people have the same birthday.

Explanation:

There are only two possible outcomes: Either the people do have the same birthday or they do not. So we use the binomial probability distribution.

Binomial probability

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

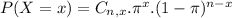
In which
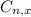`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

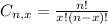
And
`\pi` is the probability of X happening.

In this problem, we have that:

There are 365 days in a year, so the probability that a person has a birthdday on any given day is given by
`\pi = (1)/(365) = 0.0027`.

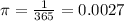Suppose there is a room with 9 people in it, find the probability that at least two people have the same birthday.

There are 9 people, so
`n = 9`.

We also want to find
`P(X > 1)`

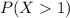
And

`P(X \leq 1) + P(X > 1) = 1`

`P(X > 1) = 1 - P(X \leq 1)`

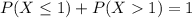
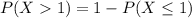
We also have that:

`P(X \leq 1) = P(X = 0) + P(X = 1)`

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

`P(X = 0) = C_(9,0).(0.0027)^(0).(0.9973)^(9) = 0.9760`

`P(X = 1) = C_(9,1).(0.0027)^(1).(0.9973)^(8) = 0.0238`

--------

`P(X \leq 1) = P(X = 0) + P(X = 1) = 0.9760 + 0.0238 = 0.9998`

`P(X > 1) = 1 - P(X \leq 1) = 1 - 0.9998 = 0.0002`

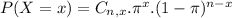
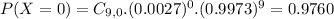
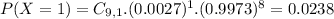
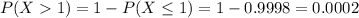
There is a 0.02% probability that at least two people have the same birthday.