Question

slader the cross section of a 5-ft long trough is an isosceles trapezoid with a 2 foot lower base, a 3-foot upper base, and an altitude of 2 feet. water is running into the trough at a rate of 1 cubic foot per minute. how fast is the water level rising when the water is 1 foot deep? slader

Answer 1

0.08 ft/min

Step-by-step explanation:

To get the speed at witch the water raising at a given point we need to know the area it needs to fill at that point in the trough (the longitudinal section), which is given by the height at that point.

So we need to get the lenght of the sides for a height of 1 foot. Given the geometry of the trough, one side is the depth d and the other (lets call it l) is given by:

`l=(3-2)/(2)\,ft+2\,ft\\l=2.5\,ft`

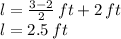
since the difference between the upper and lower base is the increase in the base and we are only at halft the height.

Now we can calculate the longitudinal section A at that point:

`A=d* l\\A=5\,ft * 2.5\, ft\\A=12.5\, ft^(2)`

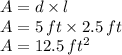
And the raising speed v of the water is given by:

`v=(q)/(A)\\v=(1\, (ft^3)/(min))/(12.5\, ft^2)\\v=0.08\, (ft)/(min)`

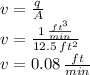
where q is the water flow (1 cubic foot per minute).