Question

A pressure gauge at the top of a vertical oil well registers 140 bars (=14 MPa). The oil well is 6000 m deep and filled with natural gas down to a depth of 4700 m and filled with oil (density=700 kg/m') the rest of the way to the bottom of the well at 15°C. The compressibility factor Z=0.80 for natural gas and its molecular weight is 18.9. Determine the pressure at (a) the natural gas-oil interface and at (b) the bottom of the well at 15°C.

Answer 1

a) 336.6 MPa

b) 345.87 MPa

Step-by-step explanation:

Given:

Pressure at the top of a vertical oil well = 140 bars =14 MPa

Depth of the oil well = 6000 m

Depth of the natural gas = 4700 m

Density of oil, ρ = 700 kg/m³

Temperature at the bottom of the well, T = 15° C = 15 + 273 = 288 K

Compressibility factor for natural gas, Z=0.80

molecular weight of natural gas = 18.9

Now,

Z=
`\frac{\textup{PV}}{\textup{RT}}`

P is the pressure 14 MPa = 14000000 Pa

V is the volume

T is the temperature

R is the ideal gas constant = 8.314 J / (mol·K)

on substituting the respective values, we get

0.80 =
`\frac{14000000*\textup{V}}{8.314*\textup{288}}`

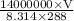
or

V = 1.36 × 10⁻⁴ m³

Now,

Assuming for 1 kg of natural gas

Density of natural gas will be equal to reciprocal of the volume obtained i.e

Density of gas =
`\frac{\textup{1}}{\textup{1.36}*10^(-4)}`

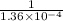
or

Density of gas, ρₐ = 7308.62 Kg/m3

Therefore,

a) Pressure at natural gas-oil interface

P₁ = ρₐ × g × h

at the interface, h = 4700 m.

therefore,

Pressure at natural gas-oil interface, P₁ = 7308.62 × 9.81 × 4700

= 336949956 Pa

= 336.6 MPa

b) Pressure at the bottom of the well, P = P₁ + ( ρₐ × g × (6000 - 4700) )

or

P = 336949956 + ( 700 × 9.81 × (6000 - 4700) )

or

P = 345877056 Pa

or

P = 345.87 MPa