Question

For budgeting purposes, the Vehicle Maintenance Manager for a municipal water and sewer utility needs to know how long the brakes on service trucks will last (in miles) before requiring replacement. The maintenance records for 20 trucks indicate that the mean life is 28,536 miles with a standard deviation of 861 miles. Based on this sample, construct a 95% confidence interval for the true population mean for brake life.

Answer 1

[ 28,133, 28,939 ]

Step-by-step explanation:

Given:

Number of trucks, n = 20

Mean life, μ = 28,536 miles

Standard deviation = 861 miles

Confidence level of interval = 95%

Now,

degree of freedom, df = n - 1

or

df = 20 - 1

or

df = 19

From the TINV function

t* = TINV ( P , df )

here P = 0.05 for 95% confidence

t* = TINV ( 0.05 , 19 )

or

t* = 2.093

Therefore,

The Margin of error =
`t*(\sigma)/(√(n))`

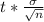
on substituting the respective values, we have

The Margin of error =
`2.093(861)/(√(20))`

or

The margin of error = 402.955 ≈ 403

Hence,

For 95% confidence, The interval for population mean will be

= Mean ± Margin of error

= 28,536 ± 403

or

the interval will be

= [ 28,536 - 403 , 28,536 + 403 ]

= [ 28,133, 28,939 ]