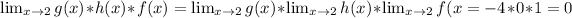Question

Given that lim x → 2 f ( x ) = 1 lim x → 2 g ( x ) = − 4 lim x → 2 h ( x ) = 0 limx→2f(x)=1 limx→2g(x)=-4 limx→2h(x)=0, find the limits, if they exist. (If an answer does not exist, enter DNE.) (a) lim x → 2 [ f ( x ) + 5 g ( x ) ] limx→2[f(x)+5g(x)] (b) lim x → 2 [ g ( x ) ] 3 limx→2[g(x)]3 (c) lim x → 2 √ f ( x ) limx→2f(x) (d) lim x → 2 4 f ( x ) g ( x ) limx→24f(x)g(x) (e) lim x → 2 g ( x ) h ( x ) limx→2g(x)h(x) (f) lim x → 2 g ( x ) h ( x ) f ( x ) limx→2g(x)h(x)f(x)

Answer 1

According what I can read, I have the following statements:

`\lim_(x \to 2) f(x) = 1`

`\lim_(x \to 2) g(x) = -4`

`\lim_(x \to 2) h(x) = 0`

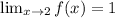
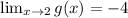
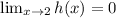
a) Applying properties of limits

`\lim_(x \to 2) f(x) + 5g(x) =  \lim_(x \to 2) f(x) + 5  \lim_(x \to 2) g(x) = 1 + 5*-4 = -19`

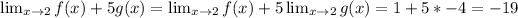
b) Applying properties of limits

`\lim_(x \to 2) g(x)^(3) = {(\lim_(x \to 2) g(x))}^(3) = (-4)^(3) = -64`

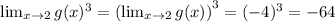
c) Applying properties of limits

`\lim_(x \to 2) √(f(x)) = \sqrt{\lim_(x \to 2) f(x)} = √(1) = 1`

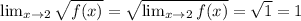
d) Applying properties of limits

`\lim_(x \to 2) 4*g(x)*f(x) = 4*\lim_(x \to 2) g(x)*\lim_(x \to 2) f(x) = 4*-4*1 =-16`

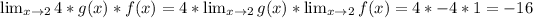
e) Applying properties of limits

`\lim_(x \to 2) g(x)*h(x) = \lim_(x \to 2) g(x)*\lim_(x \to 2) h(x) = -4*0 =0`

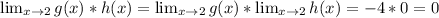
f) Applying properties of limits

`\lim_(x \to 2) g(x)*h(x)*f(x) = \lim_(x \to 2) g(x)*\lim_(x \to 2) h(x)*\lim_(x \to 2) f(x = -4*0*1 =0`