Question

In 2012 your car was worth $10,000. In 2014 your car was worth $8,800. Suppose the value of your car decreased at a constant rate of change. Define a function f to determine the value of your car (in dollars) in terms of the number of years t since 2012. f ( t ) = Suppose the value of your car decreased exponentially. Write a function g to determine the value of your car (in dollars) in terms of the number of years t since 2012. g ( t ) =

Answer 1

g(t) = 10000(0.938)^t

Explanation:

Given data:

car worth is $10,000 in 2012

car worth is $8000 in 2014

let linear function is given as

P(t) = at + b

which denote the value of car in year t

take t =0 for year 2012

at t =0, 10,000 = 0 + b

we get b = 10,000

take t =2 for year 2014

at t =2, P(2) = 2a + b

8800 = 2a + 10,000

a = - 600

Thus the price of car at year t after 2012 is given as p(t) = -600t + 10000

let the exponential function
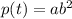`p(t)  =ab^2` where t denote t = 0 at 2012

putting t = 0 P(0) = 10,000 we get 10,000 = ab^0

a = 10,000

putting t = 2 p = 8800

`8800 =ab^2`

`b^2 = (8800)/(10000)`

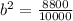
b = 0.938

g(t) = 10000(0.938)^t