Question

Goranson and Hall (1980) explain that the probability of detecting a crack in an airplane wing is the product of p1, the probability of inspecting a plane with a wing crack; p2, the probability of inspecting the detail in which the crack is located; and p3, the probability of detecting the damage. a What assumptions justify the multiplication of these probabilities? b Suppose p1 = .9, p2 = .8, and p3 = .5 for a certain fleet of planes. If three planes are inspected from this fleet, find the probability that a wing crack will be detected on at least one of them.

Answer 1

a. The multiplication of these probabilities is justified because the inspections are isolated or don't have the same goal. For instance p1, would mean that not all the planes are checked, p2 that not all the parts in the plane are checked, and p3, that even if the the part where the crack could be inspected, people checking it could not notice it or it could be not identified easily.

b. As the events are independent and there are only two possible answers (detect the plane or not), a binomial distribution could be applied, therefore:

p=0.9*0.8*.5=36 (probability of detecting the crack)

n=3 (number of possibilities, in this case number of planes)

The probability in a binomial formula is given by

`P(X=x)=(n!)/((n-x)!x!)*p^(x)*(1-p)^(n-x)`

Considering that the only possibility that is not being asked is the one of not detecting any crack which would mean x=0, then, we could find the probability as

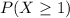`P(X\geq 1)`=1-
`P(X=0)`

`P(X\geq 1)=1-P(X=0)=1-(3!)/(3!0!) *0.36^(0) *0.64^(3) =0.737856`

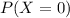
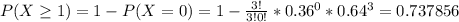
Probability is then 0.737856

Explanation: