Question

This problem has been solved!

See the answer
Find the​ (a) mean,​ (b) median,​ (c) mode, and​ (d) midrange for the data and then​ (e) answer the given question.

Listed below are the jersey numbers of
1111
players randomly selected from the roster of a championship sports team. What do the results tell​ us?
6060    
3131    
1919    
5555    
2121    
3737    
9494    
6262    
4141    
1515    
3434
a. Find the mean.
The mean is
nothing.
​(Type an integer or a decimal rounded to one decimal place as​needed.)
b. Find the median.
The median is
nothing.
​(Type an integer or a decimal rounded to one decimal place as​needed.)
c. Find the mode.
Select the correct choice below​ and, if​ necessary, fill in the answer box to complete your choice.
A.
The​ mode(s) is(are)
nothing.
​(Type an integer or a decimal. Do not round. Use a comma to separate answers as​ needed.)
B.
There is no mode.
d. Find the midrange.
The midrange is
nothing.
​(Type an integer or a decimal rounded to one decimal place as​needed.)
e. What do the results tell​ us?
A.
Since only

1111

of the jersey numbers were in the​ sample, the statistics cannot give any meaningful results.

B.

The mean and median give two different interpretations of the average​ (or typical) jersey​ number, while the midrange shows the spread of possible jersey numbers.

C.

The jersey numbers are nominal data and they do not measure or count​ anything, so the resulting statistics are meaningless.

D.

The midrange gives the average​ (or typical) jersey​ number, while the mean and median give two different interpretations of the spread of possible jersey numbers

Answer 1

(a) Mean = 42.6

(b) Median = 37

(c) Mode = Multimodal, All observation has same frequency.

(d) Midrange = 31.5

(e) B. The mean and median give two different interpretations of the average​ (or typical) jersey​ number, while the midrange shows the spread of possible jersey numbers.

Explanation:

The formula used for calculating mean is:

(a) Mean =
`\frac{\text{Sum of all the observation}}{\text{Total number of observtions}} \\=(60+31+19+55+21+37+94+62+41+15+34)/(11) \\\Rightarrow Mean = 42.6`

(b) Median is the middle observation after arranging the data in ascending or descending order.

Median is calculate by following steps:

Arranging the data in ascending order: 15, 19, 21, 31, 34, 37, 41, 55, 60, 62, 94.

Median =
`((11+1)/(2))^(th) term = 6^(th) term = 37`

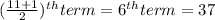
(c) Mode is the observation that has highest number of repetitions.

Here every observation has one frequency. So it is multimodal data.

(d) Midrange is also known as Quartile. And it is calculated as difference of Third Quartile to the First Quartile.

Further, Third Quartile is the middle value of Median and Last value of the observation of ascending order data.

Third Quartile = Q₃ = 57.50

First Quartile is the middle value of the First Value and Median of the observation of ascending order data.

First Quartile = Q₁ = 26

∴ Midrange = 57.50 - 26 = 31.5

(e) Mean, Median and Mode are the three of measure of central tendency from five measure of central tendency and Midrange is used to calculate dispersion\spread\scatter of data. Thus, Option B is only correct option.