Question

Slippery Elum is a baseball pitcher who uses three pitches, 60% fastballs, 25% curveballs, and the rest spitballs. Slippery is pretty accurate with his fastball (about 70% are strikes), less accurate with his curveball (50% strikes), and very wild with his spitball (only 30% strikes). Slippery ends one game with a strike on the last pitch he throws. What is the probability that pitch was a curveball?

Answer 1

There is a 21.19% that the last pitch was a curveball

Explanation:

Slippery throws the following percentage of pitches:

60% fastballs

25% curveballs

100% - (60% + 25%) = 15% spitballs.

For each pitch, he throws the following percentage of strikes

70% of the fastballs

50% of the curveballs

30% of the spitballs.

Slippery ends one game with a strike on the last pitch he throws. What is the probability that pitch was a curveball?

This question can be solved as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

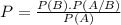
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

So

What is the probability that the pitch was a curveball, given that it is a strike?

P(B) is the probability that the pitch was a curveball. So P(B) = 0.25

P(A/B) is the probability that the pitch was a strike, given that it was a curveball. So P(A/B) = 0.5

P(A) is the probability that the pitch was a strike. He throws 60% fastballs, of which 70% are for strikes. He throws 25% curveballs, of which 50% are for strikes. And 15% spitballs, of which 30% are for strikes. So

P(A) = 0.60(0.70) + 0.25(0.50) + 0.15(0.30) = 0.59

Finally

`P = (P(B).P(A/B))/(P(A)) = (0.25*0.5)/(0.59) = 0.2119`

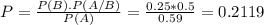
There is a 21.19% that the last pitch was a curveball