Answer:
Part 1)

Part 2)

Part 3)

Explanation:
Part 1) Write a constant of proportionality equation for this relationship
Let
y ----> the number of trains
x ----> the time minutes
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
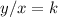 or
or

In this problem we have
For x=48 min, y=3 trains
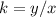 ---->
---->
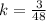
Simplify

The units of the constant of proportionality are
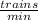
so

The linear equation is

Part 2) Given the relationship is the same, how many minute have passed after 10 trains have left the station?
For y=10 trains
substitute the value of y in the equation and solve for x


Part 3) Given the relationship is the same, how many trains have left the station after 8 hours?
For x=8 hours
substitute the value of x in the equation and solve for y
But first convert hours to minutes
remember that
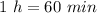
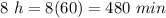
substitute
