Question

Asteroid A has a mass of 1.70×10^20 kilograms (kg), and asteroid B has a mass of 9.50×10^18 kg. Assuming that the same force was applied to both (a shock wave from a supernova, for example), what would be the ratio of A’s acceleration to B’s acceleration?

Answer 1

The ratio of asteroid-A’s acceleration to asteroid-B’s acceleration is 19:340.

Step-by-step explanation:

Mass of asteroid-A = m =
`1.70* 10^(20) kg`

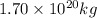
Mass of asteroid-B = m' =
`9.50* 10^(18) kg`

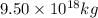
As we know , Force = mass × Acceleration

Force on asteroid-A

`F = m* a`

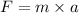
where , a is the acceleration with which asteroid-A is moving

Force on asteroid-B

`F' = m'* a'`

where , a' is the acceleration with which asteroid-B is moving

Same force is exerted on the both the asteroids say F.

F = F'

`m* a=m'* a'`

`(a)/(a')=(9.50* 10^(18) kg)/(1.70* 10^(20) kg)=(19)/(340)`

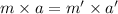
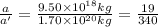
The ratio of asteroid-A’s acceleration to asteroid-B’s acceleration is 19:340.