Question

Human visual inspection of solder joints on printed circuit boards can be very subjective. Part of the problem stems from the numerous types of solder defects (e.g., pad non-wetting, knee visibility, voids) and even the degree to which a joint possesses one or more of these defects. Consequently, even highly trained inspectors can disagree on the disposition of a particular joint. In one batch of 10,000 joints, inspector A found 748 that were judged defective, inspector B found 754 such joints, and 934 of the joints were judged defective by at least one of the inspectors. Suppose that one of the 10,000 joints is randomly selected. (a) What is the probability that the selected joint was judged to be defective by neither of the two inspectors? (Enter your answer to four decimal places.)

(b) What is the probability that the selected joint was judged to be defective by inspector B but not by inspector A? (Enter your answer to four decimal places.)

Answer 1

a) There is a 90.66% probability that the selected joint was judged to be defective by neither of the two inspectors.

b) There is a 1.86% probability that the selected joint was judged to be defective by inspector B but not by inspector A.

Explanation:

The first step to solve this problem is building the "Venn Diagram" of these values.

I am going to say that we have these following values:

A is the number of pieces that inspector A found defective

B is the number of pieces that inspector B found defective.

C is the number of pieces that none of the inspector found defective.

We have that:

`A = a + (A \cap B)`

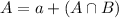
In which a are those pieces who only inspector A found defective and
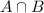`A \cap B` are those who were found to be defective by both inspectors.

By the same logic, we have that

`B = b + (A \cap B)`

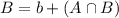
In which b are those who only rented for personal reasons.

There are 10,000 joints, so:

`a + b + (A \cap B) + C = 10,000`

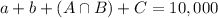
934 of the joints were judged defective by at least one of the inspectors. So:

`a + b + (A \cap B) = 934`

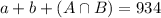
(a) What is the probability that the selected joint was judged to be defective by neither of the two inspectors?

This C(number of joints judged to not be defective by both inspectors) divided by 10,000(total number of joints).

`a + b + (A \cap B) + C = 10,000`

`934 + C = 10,000`

`C = 9,066`

`P = (C)/(10,000) = (9,066)/(10,000) = 0.9066`

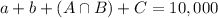
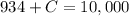
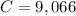
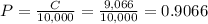
There is a 90.66% probability that the selected joint was judged to be defective by neither of the two inspectors.

(b) What is the probability that the selected joint was judged to be defective by inspector B but not by inspector A? (Enter your answer to four decimal places.)

The number of joints that are found to be defective by inspector B and not inspector A is b.

So this probability is b divided by 10,000

We have that

`a + b + (A \cap B) = 934`

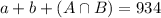
Inspector A found 748 that were judged defective, so
`A = 748`

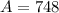
Inspector B found 754 such joints, so
`B = 754`.

`A = a + (A \cap B)`

`748 = a + (A \cap B)`

`a = 748 - (A \cap B)`

----------

`B = b + (A \cap B)`

`754 = b + (A \cap B)`

`b = 754 - (A \cap B)`

-------

`a + b + (A \cap B) = 934`

`748 - (A \cap B) + 754 - (A \cap B) + (A \cap B) = 934`

`(A \cap B) = 568`

---------

`b = 754 - (A \cap B) = 754 - 568 = 754 - 568 = 186`

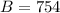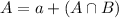
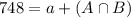
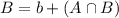
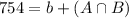
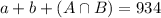
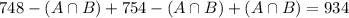
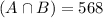
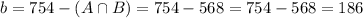
Finally:

`P = (186)/(10,000) = 0.0186`

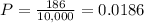
There is a 1.86% probability that the selected joint was judged to be defective by inspector B but not by inspector A.