Option A
Expression a) that is x^6- 27 is only difference of cubes out of the given expression.
Solution:
Need to find which of the expression from given four expression represents difference of cube
Let’s try to represent each term of each given expression in cubic form.
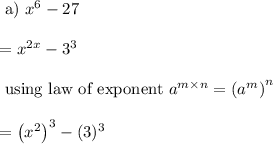
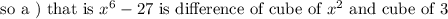
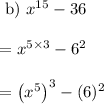
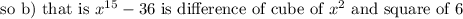
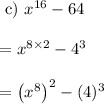
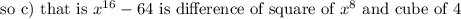

Hence we can clearly conclude that expression a) that is x^6- 27 is only difference of cubes out of the given expression.