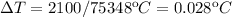Question

The pump of a water distribution system is powered by a 6-kW electric motor whose efficiency is 95 percent. The water flow rate is 18 L/s. The diameters of the inlet and outlet pipes are the same, and the elevation difference across the pump is negligible. If the pressures at the inlet and outlet of the pump are measured to be 100 kPa and 300 kPa (absolute), respectively, determine (a) the mechanical efficiency of the pump and (b) the temperature rise of water as it flows through the pump due to the mechanical inefficiency. (Answer:

Answer 1

a) Mechanical efficiency (
`\varepsilon`)=63.15% b) Temperature rise= 0.028ºC

Step-by-step explanation:

For the item a) you have to define the mechanical power introduced (Wmec) to the system and the power transferred to the water (Pw).

The power input (electric motor) is equal to the motor power multiplied by the efficiency. Thus,
`Wmec=0.95*6kW=5.7 kW`.

Then, the power transferred (Pw) to the fluid is equal to the flow rate (Q) multiplied by the pressure jump
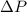`\Delta P`. So
`P_W = Q*\Delta P=0.018m^3/s * 200x10^3 Pa=3600W`.

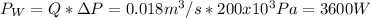The efficiency is defined as the ratio between the output energy and the input energy. Then, the mechanical efficiency is
`\varepsilon=3.6kW/5.7kW=0.6315=63.15\%`

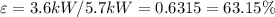
For the b) item you have to consider that the inefficiency goes to the fluid as heat. So it is necessary to use the equation of the heat capacity but in a "flux" way. Calling H to the heat transfered to the fluid, the specif heat of the water and
`\rho` the density of the water:

`[tex]H=(5.7-3.6) kW=\rho*Q*c*\Delta T=1000kg/m^3*0.018m^3/s*4186J/(kg \ºC)*\Delta T`[/tex]

Finally, the temperature rise is:

`\Delta T=2100/75348 \ºC=0.028 \ºC`