Question

3. Balancing utility and price Suppose Tim has to choose between purchasing high-definition televisions and juice. Which of the following is the utility-maximizing rule that Tim should follow while choosing the optimal quantities of these two goods? (Note: In the answer options that follow, MU stands for "marginal utility.") MU of Juice=MU of HDTVs (MU of Juice)×(Price of Juice)=(MU of HDTVs)×(Price of HDTVs) MU of JuicePrice of Juice=MU of HDTVsPrice of HDTVs MU of JuicePrice of HDTVs=MU of HDTVsPrice of Juice Since juice costs little and high-definition televisions are expensive, it must follow that when people choose their optimal quantities of juice and high-definition televisions to purchase, the marginal utility they receive from the last high-definition television they buy is than the marginal utility they receive from the last gallon of juice they buy.

Answer 1

Answer: Option (C) is correct.

Step-by-step explanation:

The following rule should be use to choose the optimal quantities of two goods:

`(MU\ of\ Juice)/(Price\ of\ Juice) =(MU\ of\ HDTVs)/(Price\ of\ HDTVs)`

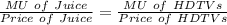
Marginal utility refers to the utility that a consumer can get from the additional unit of a commodity.

`(MU\ of\ Juice)/(MU\ of\ HDTVs) =(Price\ of\ Juice)/(Price\ of\ HDTVs)`

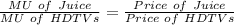
From the above equation, we can predict that marginal utility from the last TV is greater than the marginal utility obtained from the last gallon of juice. We know that Juice is less expensive as compared to the price of TV.