Answer:
a) Percentage of students scored below 300 is 1.79%.
b) Score puts someone in the 90th percentile is 638.
Explanation:
Given : Suppose a student's score on a standardize test to be a continuous random variable whose distribution follows the Normal curve.
(a) If the average test score is 510 with a standard deviation of 100 points.
To find : What percentage of students scored below 300 ?
Solution :
Mean
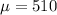 ,
,
Standard deviation
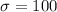
Sample mean
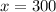
Percentage of students scored below 300 is given by,
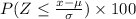
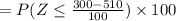
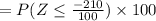

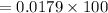
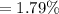
Percentage of students scored below 300 is 1.79%.
(b) What score puts someone in the 90th percentile?
90th percentile is such that,
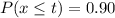
Now,
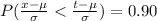
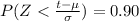
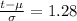
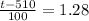
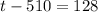
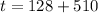

Score puts someone in the 90th percentile is 638.