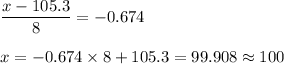Question

Tomato as a taste modifier. Miraculin—a protein naturally produced in a rare tropical fruit—has the potential to be an alternative low-calorie sweetener. In Plant Science (May 2010), a group of Japanese environmental scientists inves- tigated the ability of a hybrid tomato plant to produce mi- raculin. For a particular generation of the tomato plant, the amount x of miraculin produced (measured in micrograms per gram of fresh weight) had a mean of 105.3 and a stan- dard deviation of 8.0. Assume that x is normally distributed. a. Find P1x 7 1202. .0331 b. Find P1100 6 x 6 1102. .4677 c. Find the value a for which P1x 6 a2

Answer 1

a) 0.033

b) 0.468

c) 100

Explanation:

We are given the following information in the question:

Mean, μ = 105.3

Standard Deviation, σ = 8

The amount x of miraculin produced (measured in micro-grams per gram of fresh weight) had a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

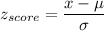
a) P(x > 120)

`P( x > 120) = P( z > \displaystyle(120 - 105.3)/(8)) = P(z > 1.8375)`

`= 1 - P(z \leq 1.8375)`

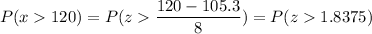
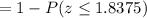
Calculation the value from standard normal z table, we have,

`P(x > 120) = 1 - 0.967 = 0.033 = 3.3\%`

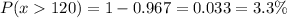
b) P(x between 100 and 110)

`P(100 \leq x \leq 110) = P(\displaystyle(100 - 105.3)/(8) \leq z \leq \displaystyle(110-105.3)/(8)) = P(-0.6625 \leq z \leq 0.5875)\\\\= P(z \leq 0.5875) - P(z \leq -0.6625)\\= 0.722 - 0.254 = 0.468 = 46.8\%`

`P(100 \leq x \leq 110) = 46.8\%`

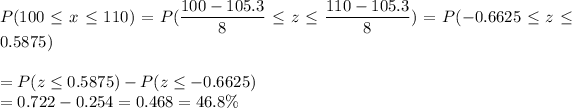
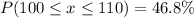
c) P(x < a) = 0.25

`P( x \leq a) = P( z \leq \displaystyle(a - 105.3)/(8)) = 0.25`

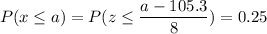
Calculation the value from standard normal z table, we have,

`P( z \leq -0.674) = 0.25`

`\displaystyle(x - 105.3)/(8) = -0.674\\\\x = -0.674* 8 + 105.3 = 99.908 \approx 100`