Question

g Based on a random sample of 25 units of product X, the average weight is 102 lb and the sample standard deviation is 10 lb. We would like to decide whether there is enough evidence to establish that the average weight for the population of product X is greater than 100 lb. Assume the population is normally distributed. Using the critical value rule, at α = .01. What is the appropriate conclusion at 99% confident level?

Answer 1

n = 25

x = 102

s = 10

Claim: the average weight for the population of product X is greater than 100 lb

`H_0 : \mu = 100\\H_a : \mu > 100`

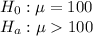
Since we are given the sample standard deviation So, we will use t test

Formula :
`t = (x-\mu)/((s)/(√(n)))`

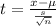
Substitute the values :

`t = (102-100)/((10)/(√(25)))`

`t = 1`

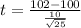
degree of freedom = n- 1 = 25-1 = 24

α = 0.01

`t_{(\alpha)/(2), df}=2.492`

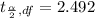
Since t critical > t calculated

So, we fail to reject null hypothesis .

So, there is no enough evidence to establish that the average weight for the population of product X is greater than 100 lb