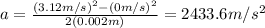Question

Froghopper insects have a typical mass of around 12.7 mg and can jump to a height of 49.3 cm. The takeoff velocity is achieved as the insect flexes its legs over a distance of approximately 2.00 mm. Assume that the jump is vertical and that the froghopper undergoes constant acceleration while its feet are in contact with the ground. Ignore air resistance. What is the acceleration of the insect during the time of the jump (before it leaves the ground)?

Answer 1

`a=2433.6m/s^2`

Step-by-step explanation:

We need to calculate at which velocity the insect departs the ground
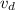`v_d`. For this we will use the formula
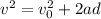`v^2=v_0^2+2ad`, where our initial velocity is our departure velocity, so
`v^2=v_d^2+2ad`.

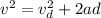Since we have the height reached and the velocity at that maximum height is 0m/s, we solve the equation for that situation, taking the upwards direction as positive and converting to S.I. we have:

`v_d=√(v^2-2ad)=√((0m/s)-2(-9.8m/s^2)(0.493cm))=3.12m/s`.

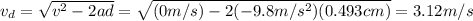We need to know the acceleration of the insect during the time of the jump (before it leaves the ground!). We know that to achieve the departure velocity (final velocity on this part) it starts from rest and the acceleration lasts while its legs move 0.002m. We use the same formula as before, but now solved for acceleration:

`a=(v^2-v_0^2)/(2d)`

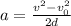
Since our final velocity will be the departure velocity now, everything starts from rest, and it moves 0.002m, we have:

`a=((3.12m/s)^2-(0m/s)^2)/(2(0.002m))=2433.6m/s^2`