Answer:
2.
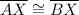
3.
 - definition of perpendicular
- definition of perpendicular
4.
 - all right angles are congruent
- all right angles are congruent
6.

7.
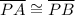
Explanation:
Given: Point P is the perpendicular bisector of AB
Prove: P is equidistant from the endpoints AB
Proof.
1. Point P is on the perpendicular bisector of AB - given
2.
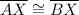 - definition of bisector
- definition of bisector
3.
 - definition of perpendicular
- definition of perpendicular
4.
 - all right angles are congruent
- all right angles are congruent
5.
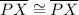 - reflexive property of congruence
- reflexive property of congruence
6.
 - SAS congruency postulate
- SAS congruency postulate
7.
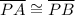 - corresponding parts of congruent triangles are congruent
- corresponding parts of congruent triangles are congruent
8. Point P is equidistant from the endpoints of AB - definition of equidistant