Question

A large operator of timeshare complexes requires anyone interested in making a purchase to first visit the site of interest. Historical data indicates that 20% of all potential purchasers select a day visit, 50% choose a one-night visit, and 30% opt for a two-night visit. In addition, 40% of day visitors ultimately make a purchase, 30% of one-night visitors buy a unit, and 50% of those visiting for two nights decide to buy. Suppose a visitor is randomly selected and is found to have made a purchase. How likely is it that this person made a day visit? (Round your answer to three decimal places.) How likely is it that this person made a one-night visit? (Round your answer to three decimal places.) How likely is it that this person made a two-night visit? (Round your answer to three decimal places.)

Answer 1

There is a 21.053% probability that this person made a day visit.

There is a 39.474% probability that this person made a one night visit.

There is a 39.474% probability that this person made a two night visit.

Explanation:

We have these following percentages

20% select a day visit

50% select a one-night visit

30% select a two-night visit

40% of the day visitors make a purchase

30% of one night visitors make a purchase

50% of two night visitors make a purchase

The first step to solve this problem is finding the probability that a randomly selected visitor makes a purchase. So:

`P = 0.2(0.4) + 0.5(0.3) + 0.3(0.5) = 0.38`

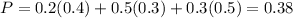
There is a 38% probability that a randomly selected visitor makes a purchase.

Now, as for the questions, we can formulate them as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

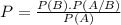
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

Suppose a visitor is randomly selected and is found to have made a purchase.

How likely is it that this person made a day visit?

What is the probability that this person made a day visit, given that she made a purchase?

P(B) is the probability that the person made a day visit. So
`P(B) = 0.20`

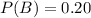
P(A/B) is the probability that the person who made a day visit made a purchase. So
`P(A/B) = 0.4`

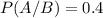
P(A) is the probability that the person made a purchase. So
`P(A) = 0.38`

So

`P = (P(B).P(A/B))/(P(A)) = (0.4*0.2)/(0.38) = 0.21053`

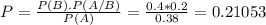
There is a 21.053% probability that this person made a day visit.

How likely is it that this person made a one-night visit?

What is the probability that this person made a one night visit, given that she made a purchase?

P(B) is the probability that the person made a one night visit. So
`P(B) = 0.50`

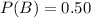
P(A/B) is the probability that the person who made a one night visit made a purchase. So
`P(A/B) = 0.3`

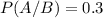
P(A) is the probability that the person made a purchase. So
`P(A) = 0.38`

So

`P = (P(B).P(A/B))/(P(A)) = (0.5*0.3)/(0.38) = 0.39474`

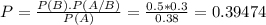
There is a 39.474% probability that this person made a one night visit.

How likely is it that this person made a two-night visit?

What is the probability that this person made a two night visit, given that she made a purchase?

P(B) is the probability that the person made a two night visit. So
`P(B) = 0.30`

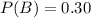
P(A/B) is the probability that the person who made a two night visit made a purchase. So
`P(A/B) = 0.5`

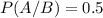
P(A) is the probability that the person made a purchase. So
`P(A) = 0.38`

So

`P = (P(B).P(A/B))/(P(A)) = (0.3*0.5)/(0.38) = 0.39474`

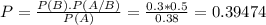
There is a 39.474% probability that this person made a two night visit.