Question

Three equal charges 2.8 µC are located in the xy-plane, one at (0 m, 68 m), another at (71 m, 0 m), and the third at (51 m,−49 m). Find the magnitude of the electric field at the origin due to these three charges. The value of Coulomb’s constant is 8.98755 × 109 N * m^2 /C^2 . Answer in units of N/C

Answer 1

E = 8.85 N/C

Step-by-step explanation:

Look at the attached graphic:

Because all the charges are positive the electric fields leave the charge towards the point P:

The electric field due to each of the charges is calculated by Coulomb's law:

E= k*q/d²

E: Electric field in N/C

q: charge in Newtons (N)

k: electric constant in N*m²/C²

d: distance from charge q to point P in meters (m)

Problem development

The electric field at a point P due to several point charges is the vector sum of the electric field due to individual charges.

E₁, E₂, E₃: Electric field at point P due to charge q₁, q₂ and q₃ respectively

q = q₁ = q₂ = q₃ = 2.8 µC = 2.8*10⁻⁶ C

K*q = 8.98755 × 10⁹ N*m²/C² * 2.8*10⁻⁶ C = 25.16*10³ N*m²/ C

E₁= k*q/d₁² = (25.16*10³)/(68)² = 5.44 N/C

E₂ = k*q/d₂² = (25.16*10³)/(71)² = 4.99 N/C

`d_3 = √(51^2+49^2) = 70.72 m`

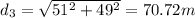
E₃ = k*q/d₃² = (25.16*10³)/(70.72)² = 5.03 N/C

Calculation of the electric field components at the origin of x-y coordinates

Eₓ = E₁ₓ+E₂ₓ+ E₃ₓ

E₁ₓ = 0

E₂x = -5 N/C

β=tan⁻¹(49/51) = 43.85°

E₃ₓ = -5.03*cos(43.85°) = -3.63 N/C

Eₓ= 0 - 5 N/C - 3.63 N/C = -8.63 N/C

Ey = E₁y + E₂y + E₃y

E₁y= -5.44 N/C

E₂y = 0

E₃y = 5.03 sin(43.85°)= 3.48 N/C

Ey = -5.44 N/C + 0 + 3.48 N/C = -1.96 N/C

Magnitude of the net electric field at the origin due q₁ ,q₂ and q₃

`E = √(E_x^2+E_y^2)`

`E = √((-8.63)^2 +(-1.96)^2)`

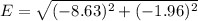
E = 8.85 N/C