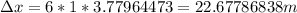Question

A dog leaps horizontally off a 70 m cliff with a speed of 6 m/s, how far from the base will the dog land?

Answer 1

`\Delta x=22.67786838m`

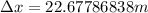
Step-by-step explanation:

Let's use projectile motion equations. First of all we need to find the travel time. So we are going to use the next equation:

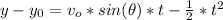`y-y_0=v_o*sin(\theta)*t-(1)/(2)*t^2` (1)

Where:

`y=Final\hspace{3}position\hspace{3}at\hspace{3}y-axis`

`y_o=Initial\hspace{3}position\hspace{3}at\hspace{3}y-axis`

`v_o=initial\hspace{3}velocity`

`t=travel\hspace{3}time`

`g=gravity\hspace{3}constant`

`\theta=Initial\hspace{3}launch\hspace{3}angle`

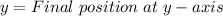
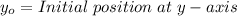
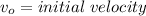
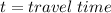
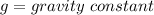
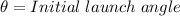
In this case:

`\theta=0`

Because the dog jumps horizontally

Let's asume the gravity constant as:

`g=9.8`

`y=0`

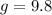
Because when the dog reach the base the height is 0

`y_o=70`

`v_o=6`

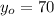
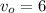
Now let's replace the data in (1)

`y_o-(1)/(2) *(9.8)*t^2+70`

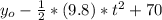
Isolating t:

`t=\pm\sqrt{(2*70)/(9.8) } =3.77964473`

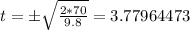
Finally let's find the horizontal displacement using this equation:

`\Delta x=v_o*cos(\theta)*t`

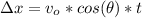
Replacing the data:

`\Delta x=6*1*3.77964473=22.67786838m`