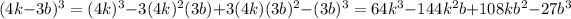Question

Which expression is equivalent to (4k−3b)3 in expanded form?

64k3−144kb2+108k2b−27b3

64k3−48k2b+36kb2−27b3

64k3−144k2b+108kb2−27b3

64k3−48kb2+36k2b−27b3

Answer 1

The correct option is C)
`64k^3-144k^2b+108kb^2-27b^3`

Explanation:

Consider the provided expression.

`\left(4k-3b\right)^3`

Apply the perfect cube formula.

`\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3`

By using the above formula.

`\left(4k\right)^3-3\left(4k\right)^2\cdot \:3b+3\cdot \:4k\left(3b\right)^2-\left(3b\right)^3`

`64k^3-144k^2b+108kb^2-27b^3`

Hence, the correct option is C)
`64k^3-144k^2b+108kb^2-27b^3`

Answer 2

Answer: THIRD OPTION.

Explanation:

You need to remember that, by definition:

`(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3`

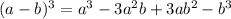
Given the following expression:

`(4k-3b)^3`

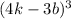
You can identify that:

`a=4k\\b=3b`

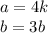
Therefore, you must substitute them into
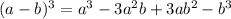`(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3` in order to find the equivalent expression for
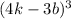`(4k-3b)^3` in expanded form.

You need to remember the Power of a power property. This states that:

`(a^m)^n=a^(mn)`

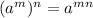
Then, you get:

`(4k - 3b)^3 = (4k)^3 - 3(4k)^2(3b) + 3(4k)(3b)^2 - (3b)^3=64k^3-144k^2b+108kb^2-27b^3`