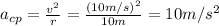Answer:
a)
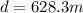
b)
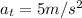
c)
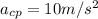
Step-by-step explanation:
a) If it did 10 revolutions, it returned to the original point, but it travelled 10 times the circunference
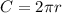 , where r is the radius of the circle, so we have
, where r is the radius of the circle, so we have
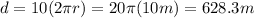
b) The tangential component of this problem can be treated as a one dimensional problem, so the (tangential) acceleration
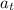 needed to reach the final speed given starting from rest after traveling a distance d can be obtained using the equation for accelerated motion
needed to reach the final speed given starting from rest after traveling a distance d can be obtained using the equation for accelerated motion
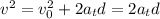 , so we have:
, so we have:
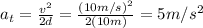
c) We use our values in the formula for centripetal acceleration given the tangential velocity and radius: