Answer:
The initial charges of the spheres were q₁=6.7712×10⁻⁶C and q₂=-4.4350×10⁻⁶C.
Step-by-step explanation:
As the spheres attract each other, the charges of the spheres are opposite.
The atracction force is given by:
F=
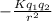
where:
K: Coulomb constant
q₁: charge of sphere 1
q₂: charge of sphere 2
r: distance between both charges
The electrostatic atraction force is 0.108 N so:
0.108N=-8.99×10⁹

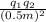
q₁·q₂=
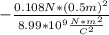
q₁·q₂=-3.003×10⁻¹² C²
When the wire is connected the charges are equally distributed as the spheres are identical. Hence, the final charge is of each sphere is

The repel force is 0.360 N and it is given by:
F=
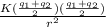
F=
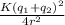
Then, we get a secong equation:
(q₁+q₂)²=
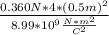
(q₁+q₂)=√4.004×10⁻¹¹ C²
q₁+q₂=6.3277×10⁻⁶ C
We solve the equation system:
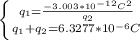
We replace q₁ in the second equation:

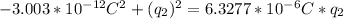
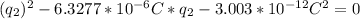
The solutions are:
q₁=6.7712×10⁻⁶C
q₂=-4.4350×10⁻⁶C