Question

When a computer disk manufacturer tests a disk, it writes to the disk and then tests it using a certifier. The certifier counts the number of missing pulses or errors. The number of errors on a test area on a disk has a Poisson distribution with ???? = 0.2. (a) What is the expected number of errors per test area? (b) What percentage of test areas have two or fewer errors?

Answer 1

Explanation:

Let X be the random variable representing the number of missing pulses or errors. The number of errors on a test area has Poisson with parameter = 0.2

a) Expected no of errors per test area =
`0.2`

(Since in a Poisson distribution mean = parameter value)

b)percentage of test areas have two or fewer errors

100*P(X≤2)

`P(X\leq 2) = P(0)+P(1)+P(2)\\= (e^(-0.2) 0.2^0)/(o!) +(e^(-0.2) 0.2^1)/(1!)+(e^(-0.2) 0.2^2)/(2!)`

`=P(X≤2)=0.99885`

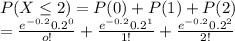
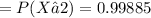
Hence percentage = 99.885%