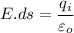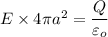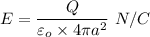Answer:
a)E= 0
b)
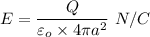
Step-by-step explanation:
Given that
Charge Q is distributed on a metallic sphere of radius a
a)r < a.
At a radius r ,from gauss theorem
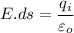
But in the sphere there is no any charge inside the sphere so
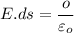
E.ds = 0
E= 0
b) r > a
At a radius r ,from gauss theorem