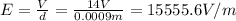Answer:
a)
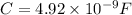
b)
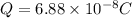
c)
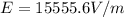
Step-by-step explanation:
a) The capacitance of a parallel-plate capacitor with plates of area A separated a distance d with a dielectric of dielectric constant k is given by the formula:
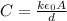
where
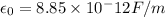 is the permittivity.
is the permittivity.
We use our values in S.I.:
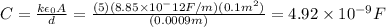
b) The charge stored Q on a capacitor of capacitance C connected to a voltage V is given by the formula Q=CV.
Using our values:
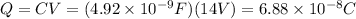
c) The electric field E between plates separated a distance d where a voltage V is applied is obtained with the formula
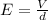 .
.
We use our values: