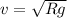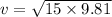Answer:
Part a)
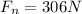
Part B)

Step-by-step explanation:
Part A)
At the top of the hump the force on the rider is
1) Normal force
2) weight
so here we know that

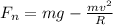
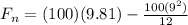
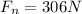
Part B)
At the top of the loop we will have
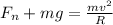
in order to remain in contact the normal force must be just greater than zero
so we will have