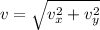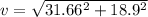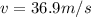Answer:
Part a)
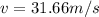
Part b)
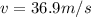
Step-by-step explanation:
Initial height of the car is 19.6 m
final height of the bridge is 1.4 m
now the vertical displacement of the car is given as
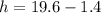
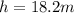
now the time taken by the car to travel the vertical distance is given as
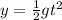

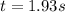
Part a)
Now the speed of the car so that it will just cross the cliff
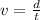
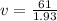
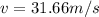
Part b)
velocity gain in y direction by the car


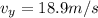
speed in x direction is given as
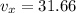
so net speed of the car is given as