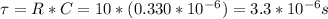Question

What is the time constant of a series circuit where the capacitor is 0.330μF and the resistor is 10Ω ?

Answer 1

`\tau=3.3*10^(-6)s`

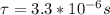
Step-by-step explanation:

Take at look to the picture I attached you, using Kirchhoff's current law we get:

`C*(dV)/(dt)+(V)/(R)=0`

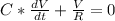
This is a separable first order differential equation, let's solve it step by step:

Express the equation this way:

`(dV)/(V)=-(1)/(RC)dt`

integrate both sides, the left side will be integrated from an initial voltage v to a final voltage V, and the right side from an initial time 0 to a final time t:

`\int\limits^V_v {(dV)/(V) } =-\int\limits^t_0 {(1)/(RC) } \, dt`

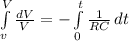
Evaluating the integrals:

`ln((V)/(v))=e^{(-t)/(RC) }`

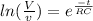
natural logarithm to both sides in order to isolate V:

`V(t)=ve^{-(t)/(RC) }`

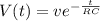
Where the term RC is called time constant and is given by:

`\tau=R*C=10*(0.330*10^(-6))=3.3*10^(-6)s`