Answer:
The time will be 25 minutes in which snowball be completely melted.
Explanation:
Given : The rate of change of the volume of a snowball that is melting is proportional to the surface area of the snowball. Suppose the snowball is perfectly spherical.
Then the volume (in centimeters cubed) of a ball of radius r centimeters is
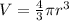
The surface area is
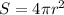
Set up the differential equation for how r is changing. Then, suppose that at time t = 0 minutes, the radius is 10 centimeters. After 5 minutes, the radius is 8 centimeters.
To find : At what time t will the snowball be completely melted?
Solution :
Using given condition,
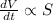
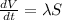 ....(1)
....(1)
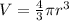
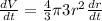
Substitute in (1),
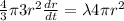
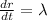

Now, t=0 , r=10
So,


i.e.
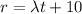
After 5 minutes, t=5 , r=8
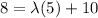
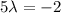
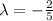
The equation form is
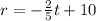
The snowball be completely melted means radius became zero.
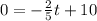
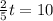
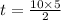

The time will be 25 minutes in which snowball be completely melted.