Question

Consider each of the following relationships. Which school shows the greatest rate of change between male and female students?

*​In school A, the ratio of male students to female students is 4:1.
*In school B, the relationship between the number of male students, y, and the number of female students, x, is given by the equation y=4/3x.
*In school C, the number of male and female students are as shown in the table.

Female students Male students
280 1260

Answer 1

The greatest ratio between male and female students is shown by School C.

Explanation:

Givens

School A:

The ratio of male students to female students is 4:1. This means there's one female student per every 4 male students.

The ratio shown here is

`r=(male)/(female)=(4)/(1)=4`

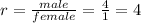
School B:

The relationshop between male students and female students is

`y=(4)/(3)x`

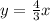
Which is a linear function, and the ratio of change is always the coefficient of the independent variable

`r=(4)/(3)`

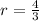
School C:

The number of males and females are shown in the table below

Female Male

280 1260

To find the ratio, we just need to divide:

`r=(male)/(female)=(1260)/(280)= 4.5`

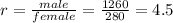
Therefore, the greatest ratio between male and female students is shown by School C.

Answer 2

School C

Explanation:

Let

y = number of male students

x = number of female students.

School A:

If the ratio of male students to female students is 4:1, then

`(y)/(x)=(4)/(1)=4`

School B:

If the relationship between y and x is given by the equation
`y=(4)/(3)x,` then

`(y)/(x)=(4)/(3)=1(1)/(3)`

School C:

The number of male and female students are as shown in the table:

`\begin{array}{lc}\text{Female students}&280\\ \\\text{Male students} &1,260\end{array}`

Then

x = 280

y = 1,260

and

`(y)/(x)=(1,260)/(280)=(126)/(28)=(63)/(14)=(9)/(2)=4.5`

The greatest rate of change is at school C, because 4.5 is the greatest number