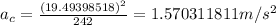Question

A car is going along a circular road at a constant speed. The radius of the curve is 242 m, and the car takes 1.3 minutes to complete one round. Calculate its centripetal acceleration in m/s^2

Answer 1

`a_c=1.57(m)/(s^2)`

Step-by-step explanation:

In order to find its centripetal acceleration we need to use the next equation:

`a_c=(v^2)/(r)`

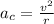
So, we need to find its velocity in first place. Considering that the time T required for one complete revolution is called the period. For constant speed is given by:

`T=(2\pi r)/(v)`

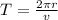
Solving for v, considering that in this case T=1.3min=78s, and r=242

`v=(2\pi *(242))/(78) =19.49398518m/s`

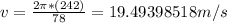
Finally, replacing v in the centripetal acceleration equation:

`a_c=((19.49398518)^(2) )/(242)=1.570311811m/s^2`