Answer:
The highest speed measured was 78.2 Mbps.
n = 50
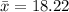
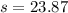
a)What is the difference between carrier's highest data speed and the mean of all 50 data speeds?
= 78.2 - 18.22
=59.98
b)How many standard deviations is that [the difference found in part (a)]
=
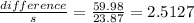
c) Convert the carrier's highest data speed to a z score.
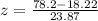
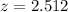
d) If we consider data speeds that convert to z scores between minus2 and 2 to be neither significantly low nor significantly high
Yes the carrier's highest data speed is significant because it is greater than 2.