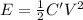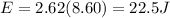Answer:
Part a)
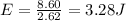
Part b)
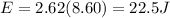
Step-by-step explanation:
As we know that the energy of capacitor when it is not connected to potential source is given as
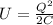
As we know that initial energy is given as
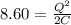
now we know that capacitance of parallel plate capacitor is given as
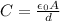
now the new capacitance when distance is changed from 3.80 mm to 1.45 mm
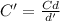

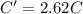
Now the new energy of the capacitor is given as
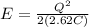
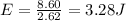
Part b)
Now if the voltage difference between the plates of capacitor is given constant
now the energy energy of capacitor is
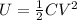
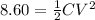
now when capacitance is changed to new value then new energy is given as