Question

An electron travels west to east with a kinetic energy of 10 keV. The Earth's magnetic field in Pittsburgh is 19,911.5 nT in the north direction, 3,257.1 nT in the west direction and 48,381.8 nT in the vertical direction. a) What is the force acting on the electron? b) What is the acceleration of the electron?

Answer 1

Step-by-step explanation:

It is given that,

Kinetic energy of the electron,
`E_k=10\ keV=10^4\ eV=1.6* 10^(-15)\ J`

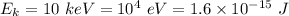
Let the east direction is +x direction, north direction is +y direction and vertical direction is +z direction.

The magnetic field in north direction,
`B_y=19911.5\ nT`

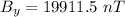
The magnetic field in west direction,
`B_x=-3257.1\ nT`

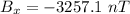
The magnetic field in vertical direction,
`B_z=48381.8 \ nT`

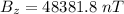
Magnetic field,
`B=(-3257.1i+19911.5j+48381.8k)\ nT`

Firstly calculating the velocity of the electron using the kinetic energy formulas as :

`E_k=(1)/(2)mv^2`

`v=\sqrt{(2E_k)/(m)}`

`v=\sqrt{(2* 1.6* 10^(-15))/(9.1* 10^(-31))}`

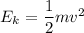
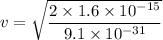
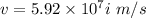`v=5.92* 10^7 i\ m/s` (as it is moving from west to east)

The force acting on the charged particle in the magnetic field is given by :

`F=q(v* B)`

`F=1.6* 10^(-19)* (5.92* 10^7 i* (-3257.1i+19911.5j+48381.8k)* 10^(-9))`

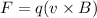
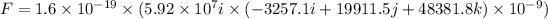
Since,
`i* j=k\ \\j* k=i\\k* i=j`

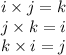
And,
`i* i=j* j=k* k=0`

`F=1.6* 10^(-19)* [1178 k-2864.20j]`

`|F|=1.6* 10^(-19)* √(1178^2+2864.20^2)`

`F=4.95* 10^(-16)\ N`

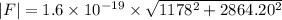
(b) Let a is the acceleration of the electron. It can be calculated as :

`a=(F)/(m)`

`a=(4.95* 10^(-16))/(9.1* 10^(-31))`

`a=5.43* 10^(14)\ m/s^2`

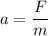
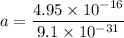
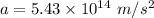
Hence, this is the required solution.