Question

An airplane covers a straight-line distance of 8.72km in 35.9 s, during which time it has a constant forward acceleration of 3.03 m/s^2. a) What is the speed of the airplane, in m/s, at the beginning of the 35.9 s? b) What is the speed of the airplane, in m/s, at the end of the 35.9 s?

Answer 1

Step-by-step explanation:

It is given that,

Distance covered by the airplane,
`d=8.72\ km=8.72* 10^3\ m`

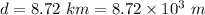
Time taken, t = 35.9 s

Acceleration of the airplane,
`a=3.03\ m/s^2`

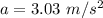
(a) Let u is the initial speed of the airplane at the beginning of the 35.9 seconds. It can be calculated using the second equation of motion as :

`d=ut+(1)/(2)at^2`

`u=(d-((1)/(2)at^2))/(t)`

`u=(8.72* 10^3-((1)/(2)* 3.03* (35.9)^2))/(35.9)`

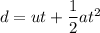
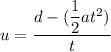
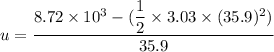
u = 188.50 m/s

(b) Let v is the speed of the airplane at the end of the 35.9 seconds. It can be calculated using the first equation of motion as :

`v=u+at`

`v=188.50+3.03* 35.9`

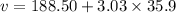
v = 297.27 m/s

Hence, this is the required solution.