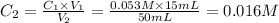Question

A chemist places 2.5316 g of Na 2SO 4 in a 100 mL volumetric flask and adds water to the mark. She then pipets 15 mL of the resulting solution into a 50 mL volumetric flask and adds water to the mark and mixes to make a solution. She then pipets 15 mL of this new solution into a 50 mL volumetric flask and dilutes to the mark. Determine the molar concentration of sodium sulfate in the most dilute solution prepared.

Answer 1

The concentration of the most dilute solution is 0.016M.

Step-by-step explanation:

First, a solution is prepared and then it undergoes two subsequent dilutions. Let us calculate initial concentration:

`[Na_(2)SO_(4)]=(moles(Na_(2)SO_(4)))/(liters(solution)) =(mass((Na_(2)SO_(4))))/(molarmass(moles(Na_(2)SO_(4)) * 0.100L)) =(2.5316g)/(142g/mol* 0.100L ) =0.178M`

First dilution

We can use the dilution rule:

C₁ x V₁ = C₂ x V₂

where

Ci are the concentrations

Vi are the volumes

1 and 2 refer to initial and final state, respectively.

In the first dilution,

C₁ = 0.178 M

V₁ = 15 mL

C₂ = unknown

V₂ = 50 mL

Then,

`C_(2)=(C_(1) * V_(1) )/(V_(2)) =(0.178M * 15mL)/(50mL) =0.053M`

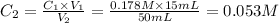
Second dilution

C₁ = 0.053 M

V₁ = 15 mL

C₂ = unknown

V₂ = 50 mL

Then,

`C_(2)=(C_(1) * V_(1) )/(V_(2)) =(0.053M * 15mL)/(50mL) =0.016M`