Question

Two small identical conducting spheres are placed with their centers 0.63 m apart. One is given a charge of 12 x 10^−9 C, the other a charge of −23 x 10^−9 C. (a) Find the electrostatic force exerted on one sphere by the other. magnitude N direction (b) The spheres are connected by a conducting wire. Find the electrostatic force between the two after equilibrium is reached, where both spheres have the same charge. magnitude N direction

Answer 1

a)
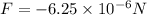`F=-6.25*10^(-6)N`, attractive.

b)
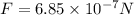`F=6.85*10^(-7)N`, repulsive.

Step-by-step explanation:

We use Coulomb's Law to calculate the electrostatic force between 2 charges
`q_1` and
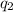`q_2` separated a distance r:

`F=(kq_1q_2)/(r^2)`

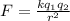
Where
`k=8.99*10^9Nm^2/C^2` is Coulomb's constant.

a) At the beginning we then have:

`F=(kq_1q_2)/(r^2)=((8.99*10^9Nm^2/C^2)(12*10^(-9)C)(-23*10^(-9)C))/((0.63 m)^2)=-6.25*10^(-6)N`

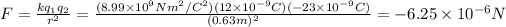
Since their signs are different it will be attractive.

b) The total charge must be conserved, which is:

`q=q_1+q_2=12*10^(-9)C-23*10^(-9)C=-11*10^(-9)C`

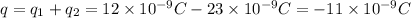
So now each charge will have a charge half this value
`q'=-5.5*10^(-9)C`

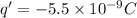
And the force will be:

`F=(kq'q')/(r^2)=((8.99*10^9Nm^2/C^2)(-5.5*10^(-9)C)(-5.5*10^(-9)C))/((0.63 m)^2)=6.85*10^(-7)N`

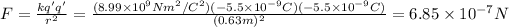
Since their signs are the same it will be repulsive.