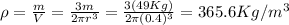Question

A hemispherical container, 31.5 inches in diameter, is filled with a liquid at 20°C and weighed. The liquid weight is found to be 1727 ounces. What is the density of the fluid in kg/m^3?

Answer 1

`\rho=365.6Kg/m^3`

Step-by-step explanation:

31.5 inches are 0.8m.

1727 ounces are 49Kg.

Our hemispherical container has a volume half of a sphere with diameter d=0.8m, or a radius r=0.4m. Since the formula for the volume of sphere is

`V_s=(4\pi r^3)/(3)`

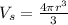
our volume will be:

`V=(1)/(2)(4\pi r^3)/(3)=(2\pi r^3)/(3)`

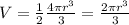
And our density can be calculated as

`\rho = (m)/(V)=(3m)/(2\pi r^3)=(3(49Kg))/(2\pi (0.4)^3)=365.6Kg/m^3`