Question

A projectile is launched at an angle of 30° and lands 20 s later at the same height as it was launched. (a) What is the initial speed of the projectile? (b) What is the maximum altitude? (c) What is the range? (d) Calculate the displacement from the point of launch to the position on its trajectory at 15 s.

Answer 1

a)Initial speed of the projectile = 196.2 m/s

b)Maximum altitude = 490.5 m

c) Range of projectile = 3398.28 m

d) Displacement from the point of launch to the position on its trajectory at 15 s = 2575.12 m

Step-by-step explanation:

Time of flight of a projectile is given by the expression,

`t=(2usin\theta)/(g)`

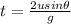
Here θ = 30° and t = 20 s

a)
`t=(2usin\theta)/(g)\\\\20=(2* usin30)/(9.81)\\\\u=196.2m/s`

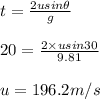
Initial speed of the projectile = 196.2 m/s

b) Maximum altitude is given by

`H=(u^2sin^2\theta)/(2g)=(196.2^2* sin^230)/(2* 9.81)=490.5m`

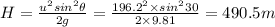
Maximum altitude = 490.5 m

c) Range of projectile is given by

`R=(u^2sin2\theta)/(g)=(196.2^2* sin(2* 30))/(9.81)=3398.28m`

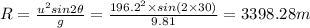
Range of projectile = 3398.28 m

d) Horizontal velocity = ucosθ = 196.2 x cos 30 = 169.91 m/s

Vertical velocity = usinθ = 196.2 x sin 30 = 98.1 m/s

We have equation of motion s = ut + 0.5 at²

Horizontal motion

u = 169.91 m/s

a = 0 m/s²

t = 15 s

Substituting

s = 169.91 x 15 + 0.5 x 0 x 15² = 2548.71 m

Vertical motion

u = 98.1 m/s

a = -9.81 m/s²

t = 15 s

Substituting

s = 98.1 x 15 + 0.5 x -9.81 x 15² = 367.88 m

`\texttt{Total displacement =}√(2548.71^2+367.88^2)=2575.12m`

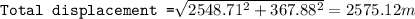
Displacement from the point of launch to the position on its trajectory at 15 s = 2575.12 m