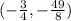Question

Find the max/min value of f(x) = 2x2 + 3x - 5

Answer 1

The minimum value is
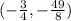`(-(3)/(4),-(49)/(8))` or
`(-0.75,-6.125)`

Explanation:

we have

`f(x)=2x^(2)+3x-5`

This is the equation a vertical parabola open upward

The vertex represent a minimum

The general equation in vertex form is

`f(x)=a(x-h)^2+k`

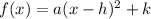
where

(h,k) is the vertex

Convert the given function in vertex form

`f(x)=2x^(2)+3x-5`

Factor 2

`f(x)=2(x^(2)+(3)/(2)x)-5`

Complete the square

`f(x)=2(x^(2)+(3)/(2)x+(9)/(16))-5-(9)/(8)`

`f(x)=2(x^(2)+(3)/(2)x+(9)/(16))-(49)/(8)`

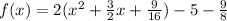
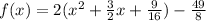
Rewrite as perfect squares

`f(x)=2(x+(3)/(4))^(2)-(49)/(8)`

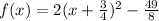
The vertex is the point
`(-(3)/(4),-(49)/(8))`