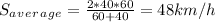Question

A car moves uphill at 40 km/h and then back downhill at 60 km/h. What is the average speed for the round trip?

Answer 1

`S_a_v_e_r_a_g_e=48km/h`

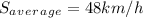
Step-by-step explanation:

Ok, the average speed can be calculate with the next equation:

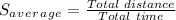`S_a_v_e_r_a_g_e=\frac{Total\hspace{3}distance}{Total\hspace{3}time}` (1)

Basically the car cover the same distance "d" two times, but at different speeds, so:

`Total\hspace{3}distance=2*d`

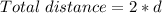
and the total time would be the time t1 required to go from A to B plus the time t2 required to go back from B to A:

`Total\hspace{3}time=t1+t2`

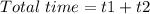
From basic physics we know:

`t=(d)/(S1)`

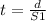
so:

`t1=(d)/(S1)`

`t2=(d)/(S2)`

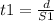
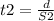
Using the previous information in equation (1)

`S_a_v_e_r_a_g_e=(2*d)/((d)/(S1) +(d)/(S2) )=(2*d)/((d*S2+d*S1)/(S1+S2) )`

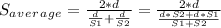
Factoring:

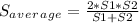`S_a_v_e_r_a_g_e=(2*S1*S2)/(S1+S2)` (2)

Finally, replacing the data in (2)

`S_a_v_e_r_a_g_e=(2*40*60)/(60+40) =48km/h`