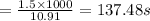Answer:137.48 s
Step-by-step explanation:
Given
Width of river=1.5 km
velocity of river=5 km/h
velocity of boat w.r.t river =12 km/h
To cross the river in minimum time hunter needs to cross the river perpendicular to the flow
i.e. velocity of boat w.r.t water must be perpendicular
i.e. x component of boat must be equal to river flow
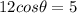
where
 is angle made by boat w.r.t bank
is angle made by boat w.r.t bank
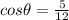

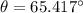
its vertical component is
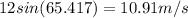
Time taken